#03 | Train Test Split for Model Selection

© Jesús López

Ask him any doubt on Twitter or LinkedIn

Chapter Importance

Machine Learning models learn a mathematical equation from historical data.

Not all Machine Learning models predict the same way; some models are better than others.

We measure how good a model is by calculating its score (accuracy).

So far, we have calculated the model's score using the same data to fit (train) the mathematical equation. That's cheating. That's overfitting.

This tutorial compares 3 different models:

Decision Tree
Logistic Regression
Support Vector Machines

We validate the models in 2 different ways:

Using the same data during training
Using 30% of the data; not used during training

To demonstrate how the selection of the best model changes if we are to validate the model with data not used during training.

For example, the image below shows the best model, when using the same data for validation, is the Decision Tree (0.86 of accuracy). Nevertheless, everything changes when the model is evaluated with data not used during training; the best model is the Logistic Regression (0.85 of accuracy). Whereas the Decision Tree only gets up to 0.80 of accuracy.

Were we a bank whose losses rank up to 1M USD due to 0.01 fail in accuracy, we would have lost 5M USD. This is something that happens in real life.

In short, banks are interested in good models to predict new potential customers. Not historical customers who have already gotten a loan and the bank knows if they were good to pay or not.

This tutorial shows you how to implement the train_test_split technique to reduce overfitting with a practical use case where we want to classify whether a person used the Internet or not.

Load the Data

Load the dataset from CIS, executing the following lines of code:

import pandas as pd #!

df_internet = pd.read_excel('https://github.com/jsulopzs/data/blob/main/internet_usage_spain.xlsx?raw=true', sheet_name=1, index_col=0)
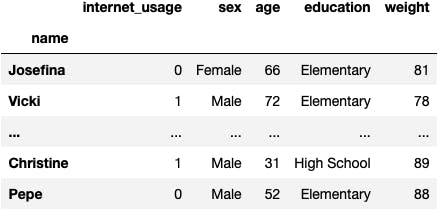
df_internet

The goal of this dataset is
To predict internet_usage of people (rows)
Based on their socio-demographical characteristics (columns)

Preprocess the Data

We should already know from the previous chapter that the data might be preprocessed before passing it to the function that computes the mathematical equation.

Missing Data

The function .fit() all the cells in the DataFrame to contain a value. NaN means "Not a Number" (i.e., cell for which we don't have any information). Otherwise, it won't know how to process the row and compare it to others.

For example, if you miss John's age, you cannot place John in the space to compare with other people because the point might be anywhere.

df_internet.isna().sum()

internet_usage    0
sex               0
age               0
education         0
dtype: int64

Dummy Variables

The function .fit() needs the values to be numeric. Otherwise, Python won't know the position of the axes in which to allocate the point. For example, if you have Male and Female, at which distance do you separate them, and why? You cannot make an objective assessment unless you separate each category.

Therefore, categories of the categorical columns will be transformed into new columns (one new column per category) and contain 1s and 0s depending on whether the person is or is not in the category.

df_internet = pd.get_dummies(df_internet, drop_first=True)
df_internet

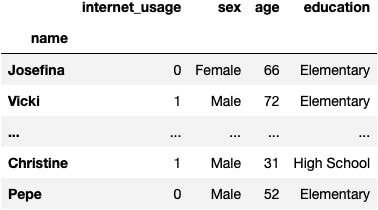
Feature Selection

Once we have preprocessed the data, we select the column we want to predict (target) and the columns we will use to explain the prediction (features/explanatory).

target = df_internet.internet_usage
features = df_internet.drop(columns='internet_usage')

Build & Compare Models' Scores

We should already know that the Machine Learning procedure is the same all the time:

Computing a mathematical equation: fit
To calculate predictions: predict
And compare them to reality: score

The only element that changes is the Class() that contains lines of code of a specific algorithm (DecisionTreeClassifier, SVC, LogisticRegression).

`DecisionTreeClassifier()` Model in Python

from sklearn.tree import DecisionTreeClassifier

model_dt = DecisionTreeClassifier()
model_dt.fit(X=features, y=target)

model_dt.score(X=features, y=target)

0.859877800407332

`SVC()` Model in Python

from sklearn.svm import SVC

model_svc = SVC(probability=True)
model_svc.fit(X=features, y=target)

model_svc.score(X=features, y=target)

0.7837067209775967

`LogisticRegression()` Model in Python

from sklearn.linear_model import LogisticRegression

model_lr = LogisticRegression(max_iter=1000)
model_lr.fit(X=features, y=target)

model_lr.score(X=features, y=target)

0.8334012219959267

Function to Automate Lines of Code

We repeated all the time the same code:

model.fit()
model.score()

Why not turn the lines into a function() to automate the process?

calculate_accuracy(model_dt)
calculate_accuracy(model_sv)
calculate_accuracy(model_lr)

To calculate the accuracy

Make a Procedure Sample for `DecisionTreeClassifier()`

model_dt = DecisionTreeClassifier()
model_dt.fit(X=features, y=target)
model_dt.score(X=features, y=target)

0.859877800407332

Automate the Procedure into a `function()`

Code Thinking

Think of the functions result
Store that object to a variable
return the result at the end
Indent the body of the function to the right
define the function():
Think of what's gonna change when you execute the function with different models
Locate the variable that you will change
Turn it into the parameter of the function()

model_dt = DecisionTreeClassifier()
model_dt.fit(X=features, y=target)
model_dt.score(X=features, y=target)

0.859877800407332

Distinguish the line that gives you the `result` you want and put it into a variable

model_dt = DecisionTreeClassifier()
model_dt.fit(X=features, y=target)
result = model_dt.score(X=features, y=target) #new

Add a line with a `return` to tell the function the object you want in the end

model_dt = DecisionTreeClassifier()
model_dt.fit(X=features, y=target)
result = model_dt.score(X=features, y=target)

return result #new

Indent everything to the right

    model_dt = DecisionTreeClassifier()
    model_dt.fit(X=features, y=target)
    result = model_dt.score(X=features, y=target)

    return result

Define the function in the first line

def calculate_accuracy(): #new

    model_dt = DecisionTreeClassifier()
    model_dt.fit(X=features, y=target)
    result = model_dt.score(X=features, y=target)

    return result

What am I gonna change every time I run the function

def calculate_accuracy(model_dt): #modified

    model_dt.fit(X=features, y=target)
    result = model_dt.score(X=features, y=target)

    return result

Generalize the name of the parameter

def calculate_accuracy(model): #modified

    model.fit(X=features, y=target) #modified
    result = model.score(X=features, y=target)

    return result

Add docstring

def calculate_accuracy(model):
    """
    This function calculates the accuracy for a given model as a parameter #modified
    """

    model.fit(X=features, y=target)
    result = model.score(X=features, y=target)

    return result

calculate_accuracy(model_dt)

0.859877800407332

Calculate Models' Accuracies

`DecisionTreeClassifier()` Accuracy

calculate_accuracy(model_dt)

0.859877800407332

We shall create an empty dictionary that keeps track of every model's score to choose the best one later.

dic_accuracy = {}
dic_accuracy['Decision Tree'] = calculate_accuracy(model_dt)

`SVC()` Accuracy

dic_accuracy['Support Vector Machines'] = calculate_accuracy(model_svc)
dic_accuracy

{'Decision Tree': 0.859877800407332,
 'Support Vector Machines': 0.7837067209775967}

`LogisticRegression()` Accuracy

dic_accuracy['Logistic Regression'] = calculate_accuracy(model_lr)
dic_accuracy

{'Decision Tree': 0.859877800407332,
 'Support Vector Machines': 0.7837067209775967,
 'Logistic Regression': 0.8334012219959267}

Which is the Best Model?

The Decision Tree is the best model with an score of 85%:

sr_accuracy = pd.Series(dic_accuracy).sort_values(ascending=False)
sr_accuracy

Decision Tree              0.859878
Logistic Regression        0.833401
Support Vector Machines    0.783707
dtype: float64

Let's suppose for a moment we are a bank to understand the importance of this chapter. A bank's business is, among other things, to give loans to people who can afford it.

Although the bank may commit mistakes: giving loans to people who cannot afford it or not giving to people who can.

Let's imagine the bank losses of £1M for each 1% of misclassification. As we chose the Decision Tree, the bank lost $15M, as the score suggests. Nevertheless, can we trust the score of 85%?

No, because we are cheating the model's evaluation; we evaluated the models with the same data used for training. In other words, the bank is not interested in evaluating the model of the historical customers; they want to know how good the model is for new customers.

They cannot create new customers. What can they do then?

They separate the data into a train set (70% of customers) used to .fit() the mathematical equation and a test set (30% of customers) to evaluate the mathematical equation.

You can understand the problem better with the following analogy:

University Access Exams Analogy

Let's imagine:

You have a math exam on Saturday
Today is Monday
You want to calibrate your level in case you need to study more for the math exam
How do you calibrate your math level?
Well, you've got 100 questions X with 100 solutions y from past years exams
You may study the 100 questions with 100 solutions fit(100questions, 100solutions)
Then, you may do a mock exam with the 100 questions predict(100questions)
And compare your_100solutions with the real_100solutions
You've got 90/100 correct answers accuracy in the mock exam
You think you are prepared for the maths exam
And when you do the real exam on Saturday, the mark is 40/100
Why? How could we have prevented this?
Solution: separate the 100 questions into 70 for train to study & 30 for test for the mock exam.
1. fit(70questions, 70answers)
2. your_30solutions = predict(30questions)
3. your_30solutions ?= 30solutions

`train_test_split()` the Data

The documentation of the function contains a typical example.

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(
    features, target, test_size=0.30, random_state=42)

What the heck is returning the function?

From all the data:

2455 rows
8 columns

df_internet

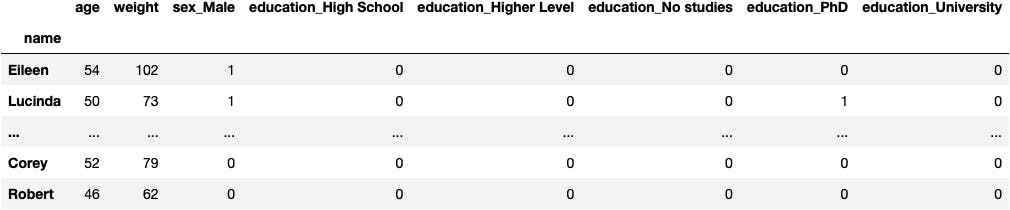
1728 rows (70% of all data) → to fit the model
7 columns (X: features variables)

X_train

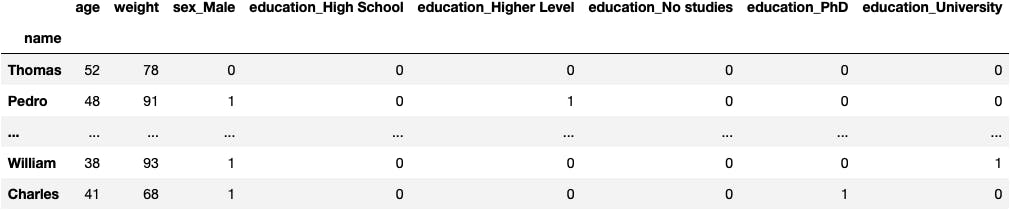
737 rows (30% of all data) → to evaluate the model
7 columns (X: features variables)

X_test

1728 rows (70% of all data) → to fit the model
1 columns (y: target variable)

y_train

name
Eileen     0
Lucinda    1
          ..
Corey      0
Robert     1
Name: internet_usage, Length: 1718, dtype: int64

737 rows (30% of all data) → to evaluate the model
1 columns (y: target variable)

y_test

name
Thomas     0
Pedro      1
          ..
William    1
Charles    1
Name: internet_usage, Length: 737, dtype: int64

`fit()` the model with Train Data

model_dt.fit(X_train, y_train)

DecisionTreeClassifier()

Compare the predictions with the real data

model_dt.score(X_test, y_test)

0.8046132971506106

Optimize All Models & Compare Again

Make a Procedure Sample for `DecisionTreeClassifier()`

model_dt = DecisionTreeClassifier()
model_dt.fit(X_train, y_train)
model_dt.score(X_test, y_test)

0.8032564450474898

Automate the Procedure into a `function()`

Code Thinking

Think of the functions result
Store that object to a variable
return the result at the end
Indent the body of the function to the right
define the function():
Think of what's gonna change when you execute the function with different models
Locate the variable that you will change
Turn it into the parameter of the function()

def calculate_accuracy_test(model):

    model.fit(X_train, y_train)
    result = model.score(X_test, y_test)

    return result

Calculate Models' Accuracies

`DecisionTreeClassifier()` Accuracy

dic_accuracy_test = {}

dic_accuracy_test['Decision Tree'] = calculate_accuracy_test(model_dt)
dic_accuracy_test

{'Decision Tree': 0.8032564450474898}

`SVC()` Accuracy

dic_accuracy_test['Support Vector Machines'] = calculate_accuracy_test(model_svc)
dic_accuracy_test

{'Decision Tree': 0.8032564450474898,
 'Support Vector Machines': 0.7788331071913162}

`LogisticRegression()` Accuracy

dic_accuracy_test['Logistic Regression'] = calculate_accuracy_test(model_lr)
dic_accuracy_test

{'Decision Tree': 0.8032564450474898,
 'Support Vector Machines': 0.7788331071913162,
 'Logistic Regression': 0.8548168249660787}

Which is the Best Model with `train_test_split()`?

The picture change quite a lot as the bank is losing £20M due to the model we chose before: the Decision Tree; the score in data that hasn't been seen during training (i.e., new customers) is 80%.

We should have chosen the Logistic Regression because it's the best model (85%) to predict new data and new customers.

In short, we lose £15M if we choose the Logistic Regression, which it's better than the Decision Tree's loss of £20M. Those £5M can make a difference in my life 👀

sr_accuracy_test = pd.Series(dic_accuracy_test).sort_values(ascending=False)
sr_accuracy_test

Logistic Regression        0.854817
Decision Tree              0.803256
Support Vector Machines    0.778833
dtype: float64

df_accuracy = pd.DataFrame({
    'Same Data': sr_accuracy,
    'Test Data': sr_accuracy_test
})

df_accuracy.style.format('{:.2f}').background_gradient()

Command Palette

Comments

Machine Learning

#01 | The Linear Regression & Supervised Regression Models

More from this blog

Chapter Importance

Load the Data

Preprocess the Data

Missing Data

Dummy Variables

Feature Selection

Build & Compare Models' Scores

DecisionTreeClassifier() Model in Python

SVC() Model in Python

LogisticRegression() Model in Python

Function to Automate Lines of Code

Make a Procedure Sample for DecisionTreeClassifier()

Automate the Procedure into a function()

Distinguish the line that gives you the result you want and put it into a variable

Add a line with a return to tell the function the object you want in the end

Indent everything to the right

Define the function in the first line

What am I gonna change every time I run the function

Generalize the name of the parameter

Add docstring

Calculate Models' Accuracies

DecisionTreeClassifier() Accuracy

SVC() Accuracy

LogisticRegression() Accuracy

Which is the Best Model?

University Access Exams Analogy

train_test_split() the Data

What the heck is returning the function?

fit() the model with Train Data

Compare the predictions with the real data

Optimize All Models & Compare Again

Make a Procedure Sample for DecisionTreeClassifier()

Automate the Procedure into a function()

Calculate Models' Accuracies

DecisionTreeClassifier() Accuracy

SVC() Accuracy

LogisticRegression() Accuracy

Which is the Best Model with train_test_split()?

`DecisionTreeClassifier()` Model in Python

`SVC()` Model in Python

`LogisticRegression()` Model in Python

Make a Procedure Sample for `DecisionTreeClassifier()`

Automate the Procedure into a `function()`

Distinguish the line that gives you the `result` you want and put it into a variable

Add a line with a `return` to tell the function the object you want in the end

`DecisionTreeClassifier()` Accuracy

`SVC()` Accuracy

`LogisticRegression()` Accuracy

`train_test_split()` the Data

`fit()` the model with Train Data

Make a Procedure Sample for `DecisionTreeClassifier()`

Automate the Procedure into a `function()`

`DecisionTreeClassifier()` Accuracy

`SVC()` Accuracy

`LogisticRegression()` Accuracy

Which is the Best Model with `train_test_split()`?